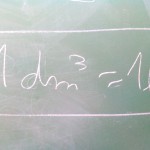Aquests dies els alumnes de 6EP hem après a calcular el volum de líquid que cap en un recipient. Per fer-ho, hem relacionat la mesura amb la geometria. Com quan parlem de volum, utilitzem unitats “cúbiques”, hem agafat un cub de plàstic i l’hem omplert d’aigua fins a dalt. Val a dir, però, que no era un cub qualsevol, sinó un cub amb 10 centímetres de costat, és a dir, 1 decímetre.
Un cop omplert, hem calculat mitjançant xeringues i una gerra que justament hi cabia 1 litre. Com a resultat, hem descobert aquesta curiosa conversió: 1 dm³ = 1l.
Conseqüència: ja no ens farà falta mullar-nos per saber quants litres caben en una piscina: només farà falta saber quants decímetres mesura cadascun dels seus costats.