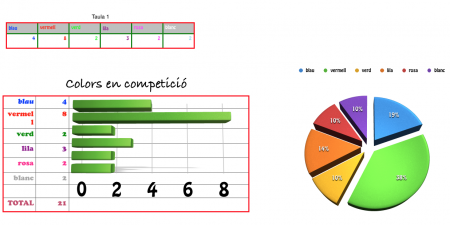
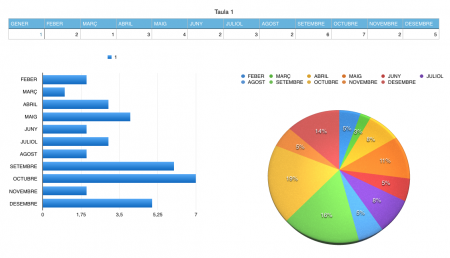
La setmana passada, els alumnes de 2EP vam estudiar els colors d’alguns collarets a la classe de matemàtiques. A alguns, al principi ens va sobtar molt: què tenen a veure els collarets amb aquesta assignatura?
Al cap de pocs minuts vam veure una primera explicació: els seus colors ens permeten estudiar diferents tipus de seriacions, quelcom que té a veure amb les “Relacions i el Canvi”.
Però, a més a més, quan portàvem ja una estona de classe, vam començar a veure que aquells collarets amagaven alguna cosa més… Si el primer color era el negre, el segon el blau, el tercer el groc, el quart el taronja i després es tornaven a repetir, era fàcil saber quins colors serien el cinquè, el sisè, el setè… Només feia falta continuar la sèrie.
Però què passa quan ens pregunten quin color serà el nombre 32? És necessari pintar els 32 colors? En realitat, els colors es van repetint seguint el mateix patró. El color 32 és el taronja, però és que el 4, el 8, el 12, el 16, el 20… també ho són. ¿Què estem estudiant, llavors, en realitat? ¿Què són tots aquests nombres de color taronja?